计算理论研究的课题是计算机的基本能力和局限是什么。主要包含三个核心领域自动机理论与形式语言，可计算性理论与计算复杂性理论。

判定问题

在可计算性理论理论中，判定问题（Entscheidungsproblem/Decision Problem）是指一个问题，其答案只有两种可能的情况：是或否。 判定问题的提法是1928年，大卫·希尔伯特（David Hilbert）和威廉·阿克曼（Wilhelm Ackermann）提出。

1900年，希尔伯特在第二届国际数学家大会上提出的23个数学问题中的第十问题，即丢番图方程问题是一个判定问题。

判定问题不存在通用解法

1935-1936，阿隆佐·邱奇引入λ演算，并证明没有任何通用算法可以判定任意两个λ表达式是否相等。证明了解决判定问题的通用算法不存在。

1936年，阿兰·图灵发明了图灵机。图灵把解决判定问题的通用解法是否存在的问题归约到停机问题。通过停机问题的不可解证明的判定问题不存在通用解法。 图灵后来证明了λ演算和图灵机是等价的计算模型。

图灵机

本节内容主要来自：Turing Machines and Computability

图灵机

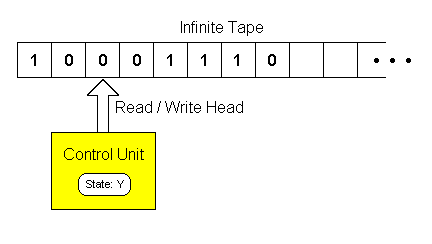
Turing Machine

  • 图灵机是数学模型而非物理模型
  • 控制单元(Control unit)可能处于某个状态，所有可能的状态是有限的
  • 每个格子包含一个符号，符号数量有限
  • 读写头每步可以修改当前位置的符号
  • 读写头每步可以向左或向右移动一格
  • 纸带长度无限

图灵机实例：位翻转 | 当前状态 | 当前符号 | 新状态 | 新符号 | 移动方向 | | 1 | 0 | 1 | 1 | R | | 1 | 1 | 1 | 0 | R | | 1 | b | 2 | b | R |

起始状态：1 结束状态：2

图灵机的功能是翻转输入的01串的每一位，如输入1100输出0011。

通用图灵机

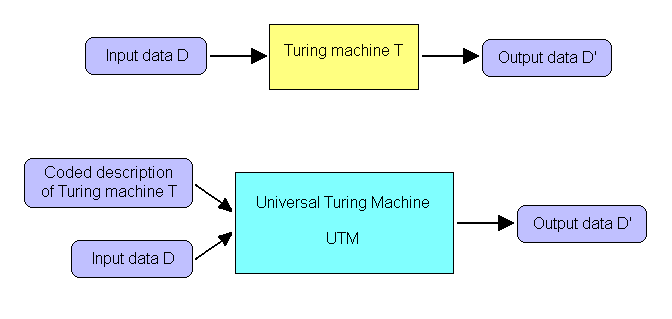
图灵机通过合适的编程，可以模拟任何其他图灵机，这种图灵机称为通用图灵机(UTM, Universal Turing Machine)。 Universial Turing Machine

  • 通用图灵机接受一个图灵机的编码描述，并模拟该图灵机在对应输入上的行为
  • 编码描述充当通用图灵机执行的程序
  • 通用图灵机本身的内部程序是固定的

存储程序计算机(Stored-program computer)

计算机可以看作通用图灵机的物理实现。当前的计算机基本都属于存储程序计算机，即把程序指令存储在主存中的计算机。 理论上，冯诺依曼架构和哈佛架构都可以认为是存储程序计算机，但是很多时候存储程序计算机会特指冯诺依曼架构。

冯诺依曼架构 (Von Neumann architecutre)把指令和数据存储在同样的内存中，而哈佛架构的指令和数据存储在不同的内存中。

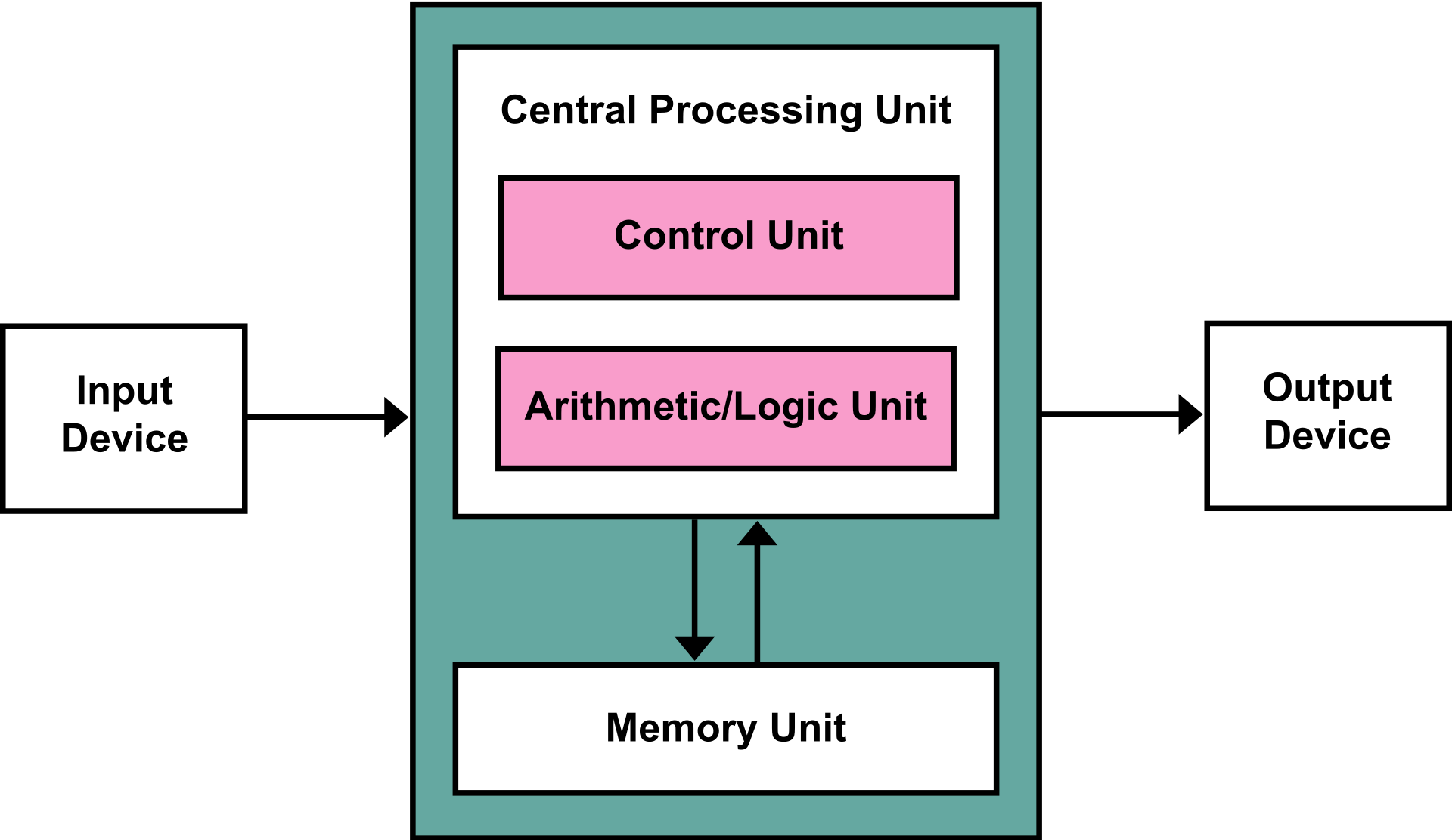
以下两个示意图来自wikipedia： Von Neumann architecutre

冯诺依曼架构

Harvard architecutre

哈佛架构

值得一提的是，现代计算机已经不是严格的冯诺依曼架构或哈佛架构，而是两者的结合。 例如x86及其的主存是共享的，但CPU的L1/L2 cache是指令和数据cache是分开的。

可计算性

邱奇-图灵论题

任何在算法上可计算的问题同样可由图灵机计算 称之为论题而非定理（thesis vs. theory），是因为该论题是对计算特性的一种描述，而不是形式化的表示，所以无法被证明。 反过来，算法的精确概念可以由此定义：算法即图灵机算法，图灵机可以在有限步骤内解决问题。

图灵可计算性也由此定义。更精确地说，一个自然数集合是可计算集合，如果存在一个图灵机，对于一个给定的数n，如果n在该集合中，图灵机停止并输出1，否则图灵机停止并输出0。 从形式语言的角度，则可以定义为：如果一个语言能被某一图灵机判定(即图灵机识别该语言并停机)，则称之为图灵可判定的。 也即，判定问题与图灵可计算性是紧密关联的。

图灵完备与图灵等价

  • 图灵完备：可以计算所有图灵可计算函数的系统是图灵完备的；换句话说，这个系统可以仿真通用图灵机
  • 图灵等价：一个图灵完备的系统，如果它可以计算算的函数都是图灵可计算的，那么称为图灵等价；即图灵等价的系统可以仿真通用图灵机，也可以用通用图灵机仿真。 目前所有已知的物理实现的图灵完备系统都是图灵等价的。

计算模型

计算模型是指对于一个输入，一个数学函数如何计算输出的模型。 图灵机，λ演算，递归函数（μ-recursive function）等都是等价的计算模型，也是目前可实现的最强的计算模型。

因为这些计算模型的局限性，数学家也提出了很多超计算模型。

References